U4. El modelo estándar de comercio

Comercio y Finanzas Internacionales [UCC]

El modelo estándar de comercio

¿Cuál modelo?

Hasta ahora hemos visto 3 (tres) modelos distintos de comercio internacional. Difieren en supuestos y también en conclusiones. Repasemos sus características
1. Modelo ricardiano \(\longrightarrow\) 1 (un) sólo factor –\(L\)-, y 2 (sectores). La asignación de \(L\) entre sectores determina la FPP. Aporta idea de ventaja comparativa pero no avanza en distribución de la renta
2. Modelo factores específicos \(\longrightarrow\) 3 (tres) factores –\(L\), \(K\) y \(T\). Foco en consecuencias distributivas a corto plazo
3. Modelo de Heckscher-Ohlin \(\longrightarrow\) 2 (dos) factores –\(L\), \(K\)- con libre movilidad. Diferencias en dotacion relativa determina patrón de comercio. Foco en consecuencias distributivas a largo plazo

Todos!

Cuando analizamos problemas, solemos tomar una combinación de los mismos. Para analizar un rapido crecimiento de \(X\) de nuevos países industrializados por razones de productividad, el modelo ricardiano es util. Para analizar consecuencias distributivas, los modelos de factores específicos y H-O son más utiles que el ricardiano
Características compartidas
1. Todos parten de posibilidades de producción (FPP) –diferencias en las FPP origen del comercio
2. FPP determinan funcion de OR de un país
3. Equilibrio mundial determinado por cruce de DR y OR mundiales, estas ultimas situadas entre OR nacionales

Modelo general

El modelo estándar de comercio se construye a partir de 4 (cuatro) relaciones clave
1. Relación entre FPP y curva de OR
2. Relación entre precios relativos y curva de DR
3. Determinación de equilibrio mundial a través de OR y DR mundiales
4. Efecto de la relación de intercambio –\(\frac{P_{X}}{P_{M}}\) sobre bienestar nacional
Modelo estándar supone:
- Cada país produce 2 (dos) bienes –\(A\) y \(T\)
- FPP es una curva cóncava

Modelo general: posibilidades de producción y OR

Modelo general: posibilidades de producción y OR (cont.)

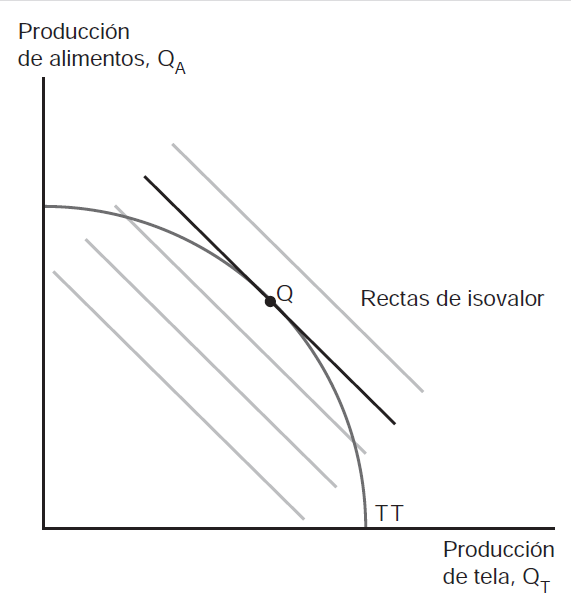
La economía produce en el punto de tangencia entre FPP y el relativo de precios, \(\frac{P_{T}}{P_{A}}\). Para precios de mercado dados economía elegirá punto de producción que aumente al máximo el valor de producción –\(P_{T}Q_{T}+P_{A}Q_{A}\)
La recta de isovalor es línea a lo largo de la cual valor de producción es constante –\(Q_{A}=\frac{V}{P_{A}}-\frac{P_{T}}{P_{A}}Q_{T}\), donde \(V\) es el valor de la producción
Si \(\frac{P_{T}}{P_{A}}\) aumenta, recta de isovalor mayor pendiente y se produce más \(T\) y menos \(A\) \(\longrightarrow\) aumenta la OR de tela, \(T\)

Modelo general: posibilidades de producción y OR (cont.)

Modelo general: precios relativos y demanda

En una economía sin comercio, el valor de la producción debe igualar el valor del consumo –por lo tanto producción y consumo deben estar en la misma curva de isovalor

\[\begin{equation} P_{T}Q_{T}+P_{A}Q_{A}=P_{T}D_{T}+P_{A}D_{A} \end{equation}\]

el punto de consumo depende de las preferencias de consumidores –curvas de indiferencia [supuestos de las CI]

Modelo general: precios relativos y demanda (cont.)

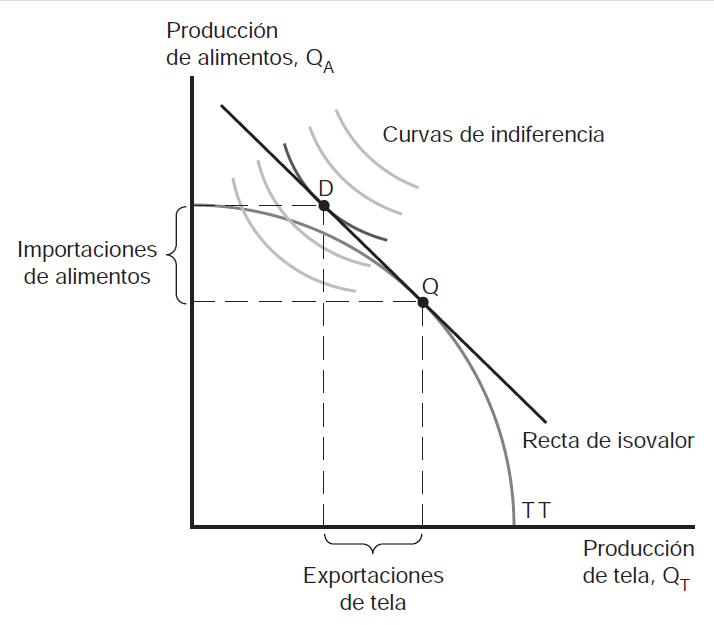
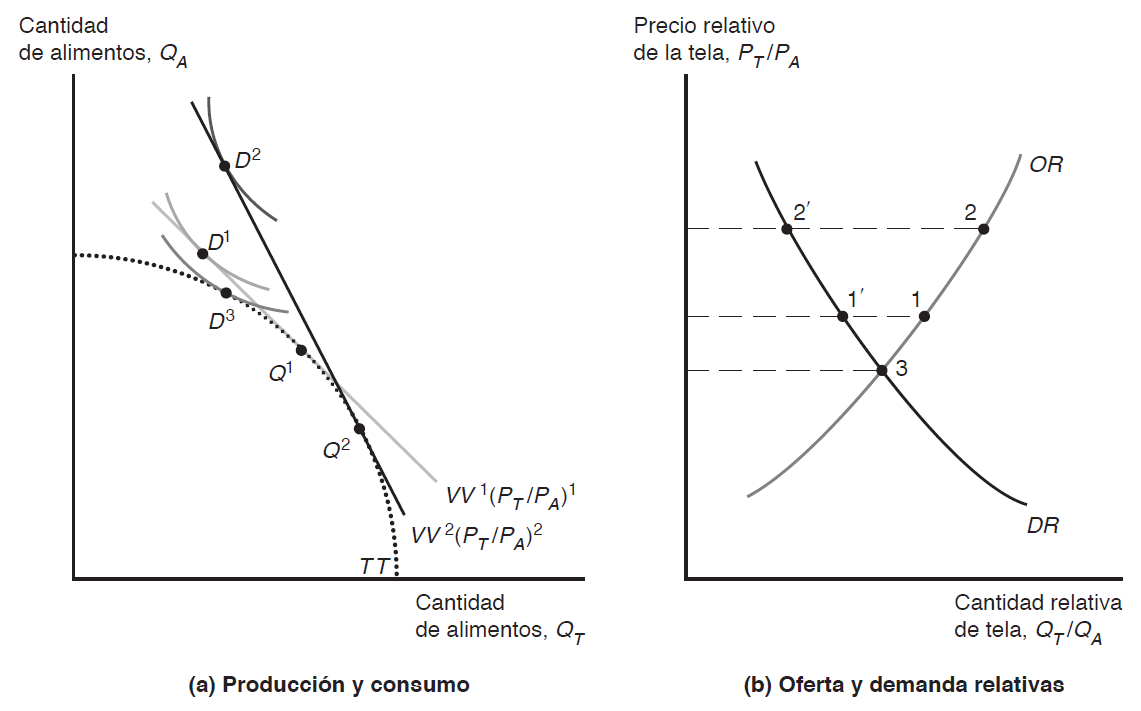
En la figura puede verse que tanto la elección de consumo como de producción están en la misma curva de isovalor (y la más alta posible) pero \(\longrightarrow\) la economía exporta \(T\) e importa \(A\) [¿por qué?]
Interesa saber que pasa cuando aumenta \(\frac{P_{T}}{P_{A}}\)
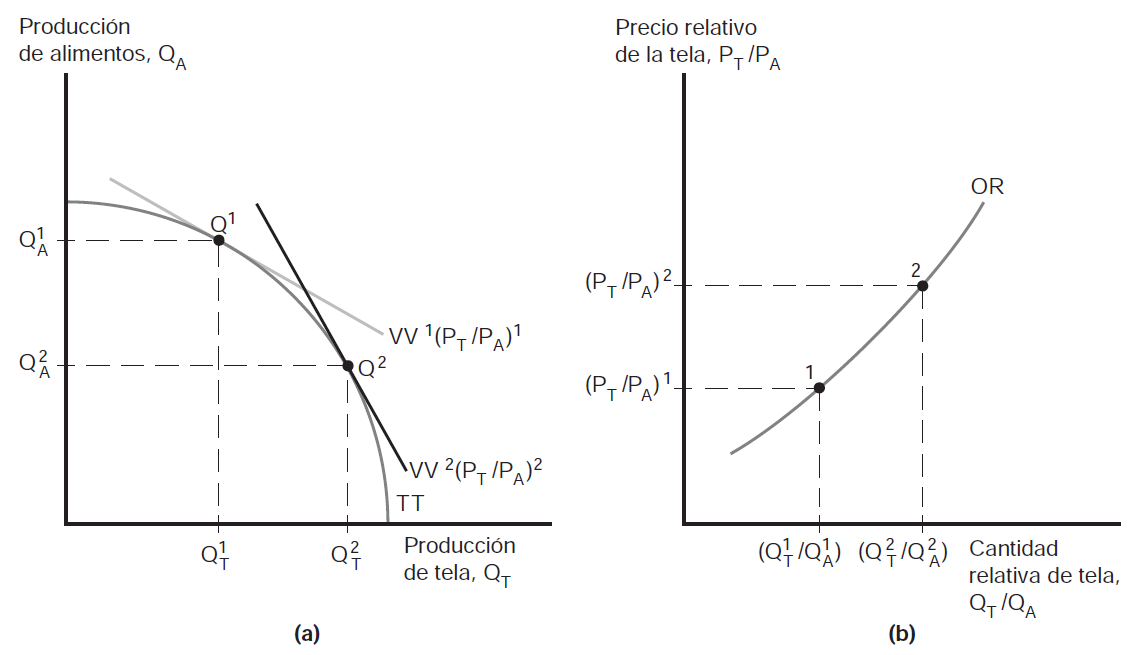
- Economía produce más \(T\) y menos \(A\) –producción de \(Q_{1}\) a \(Q_{2}\) (cambia recta de isovalor)
- Pero también cambia el consumo –consumo de \(D_{1}\) a \(D_{2}\)

Modelo general: precios relativos y demanda (cont.)

Existen 2 (dos) efectos que hacen que suceda este movimiento
- Economía se traslada a CI más alta porque al subir precio relativo de \(T\) puede tener más \(M\) para una cantidad dada de \(X\) \(\longrightarrow\) efecto ingreso
- Economía se traslada a lo a largo de la CI hacia más consumo de \(A\) y menos de \(T\) dado que tela es ahora relativamente más cara \(\longrightarrow\) efecto sustitución
Lo importante aquí es que la DR de \(T\) disminuye cuando aumenta \(P_{T}\); mientras que la OR de \(T\) aumenta cuando aumenta \(P_{T}\)
- el hecho de que la DR de tela caiga sugiere que domina el efecto sustitución
¿Si la economía no puede comerciar? Consume en el punto 3 (\(D_{3}\)) donde \(OR=DR\)

Modelo general: efectos de cambios en la relación de intercambio sobre el bienestar

Hemos visto que cuando aumenta \(\frac{P_{T}}{P_{A}}\) en un país que inicialmente exporta \(T\) mejora su situación.
Ahora, si el país fuera inicialmente exporta \(A\) el efecto se invierte \(\longrightarrow\) un aumento de \(\frac{P_{T}}{P_{A}}\) equivale a una disminución de \(\frac{P_{A}}{P_{T}}\) \(\longrightarrow\) país empeora porque baja el precio relativo del bien que exporta
Podemos definir ahora la relación de intercambio como el precio del bien que el país exporta (inicialmente) dividido el precio del bien que el país importa (inicialmente)

Modelo general: efectos de cambios en la relación de intercambio sobre el bienestar

Un aumento en la relacion de intercambio incrementa el bienestar de un país mientras que una reducción de la relación de intercambio disminuye su bienestar

Cambios en la relación de intercambio, sin embargo, no reducen el bienestar por debajo del nivel de bienestar que tendría sin comercio –en el gráfico representado por punto \(D_{3}\). Note que es el peor nivel de bienestar posible

Modelo general: determinación de los precios relativos

Nuestro país exporta \(T\) y país extranjero exporta \(A\). Relación de intercambio en nuestro país es \(\frac{P_{T}}{P_{A}}\); la del país extranjero es \(\frac{P_{A}}{P_{T}}\)
Si ambos comparten mismas curvas de DR, para cualquier precio dado \(\frac{P_{T}}{P_{A}}\), nuestro país produce \(Q_{T}\) y \(Q_{A}\) y país extranjero produce \(Q_{T}^{*}\) y \(Q_{A}^{*}\) donde \(\frac{Q_{T}}{Q_{A}} > \frac{Q_{T}^{*}}{Q_{A}^{*}}\)
Y de esa manera se obtiene la OR mundial: \(\frac{(Q_{T}+Q_{T}^{*})}{(Q_{A}+Q_{A}^{*})}\)
La DR se obtiene de manera similar, \(\frac{(D_{T}+D_{T}^{*})}{(D_{A}+D_{A}^{*})}\)