Tópicos de Economía Política (UNS)
Unidad 4. Estos son mis principios. Si no le gu$tan, tengo otros. Influencia, dinero y grupos de interés
If money go before, all ways do lie open.
[William Shakespeare, Ford, The Merry Wives of Windsor, Act 2 Scene 2 (1602)]
Financiamiento de campañas y lobbying
- Actividad pre-electoral y post-electoral
- Regulación versus desregulación
- ¿Comprando la política o comprando influencia?
Financiamiento de campañas
- ¿Y por casa cómo andamos? En Argentina, las dos leyes más importantes que regulan la actividad electoral y el financiamiento de partidos politicos son la Ley 26571 (2009) –hito principal el establecimiento de las PASO- y la Ley 26215 (2007) y sus modificatorias
- ¿El lobbying está institucionalizado en Argentina? No!
- hay algunas iniciativas pero no hay una Ley Nacional
- Régimen de Acceso a la Información Pública (2003, luego Ley 27275 (2016))
Financiamiento de campañas (cont.)
- Importante notar la deficiencia en la sistematización, publicación y difusíon de estadísticas en relación a la actividad de financiamiento partidario
- Sin embargo, algunos avances en años recientes Link: Financiamiento de Campañas - Aportes privados
- En Argentina pueden aportar personas físicas y jurídicas –ambas con limitaciones. No pueden aportar personas físicas/jurídicas extranjeras y tampoco gobiernos y entidades públicas extranjeras
Financiamiento de campañas (cont.)
Contribuciones por sectores de actividad - Personas jurídicas
Gasto en publicidad
- El gasto en publicidad tradicional –principalmente radio y TV- puede consultarse en sitios que agregan y monitorean esta información: Gasto en publicidad tradicional
- Interesante mirar también la actividad de donación y contribuciones en forma de publicidad digital –gasto en publicidad digital tomando con fuente Google y Facebook
- Recurso útil: Gasto en publicidad digital
- Interesante correlacionar el gasto en publicidad digital con ultimo resultado electoral/encuestas de intención de voto
El rol de la dark money
- En lingo especialista, dark money refiere al gasto con intención de afectar los resultados políticos en el cual la fuente/origen de los fondos no es revelado
- En EEUU esto es posible por la existencia de ONGs políticamente activas (tipología 501(c)(4)) que no tienen obligacion de declarar sus donantes
- Esto “explotó” luego de 2010 de producido el fallo de la Corte “Citizens United v. FEC Supreme Court” – que basicamente permitió la existencia y proliferació de estas grupos políticamente activos
El rol de la dark money (cont.)
Citizens United v. FEC Supreme Court. En 2007, en FEC v. Wisconsing Right to Life la Corte Suprema falló que las organizaciones sin fines de lucro podía usar fondos para publicidad antes de las elecciones siempre y cuando estas publicidades no se expresaran explícitamente a favor (o en contra) de algún candidato. En el año 2010, la Corte Suprema falló que la prohibición que pesaba sobre contribuciones politicas independientes violaba el derecho a la libre expresión contenido en la Primera Enmienda. Este fallo permitió deliberadamente el uso de fondos para publicidad que se expresara explícitamente a favor (o en contra) de algún candidato. Desde este fallo, se produjo la década de mayor gasto en campañas en la historia de los EEUU.
El rol de la dark money (cont.)
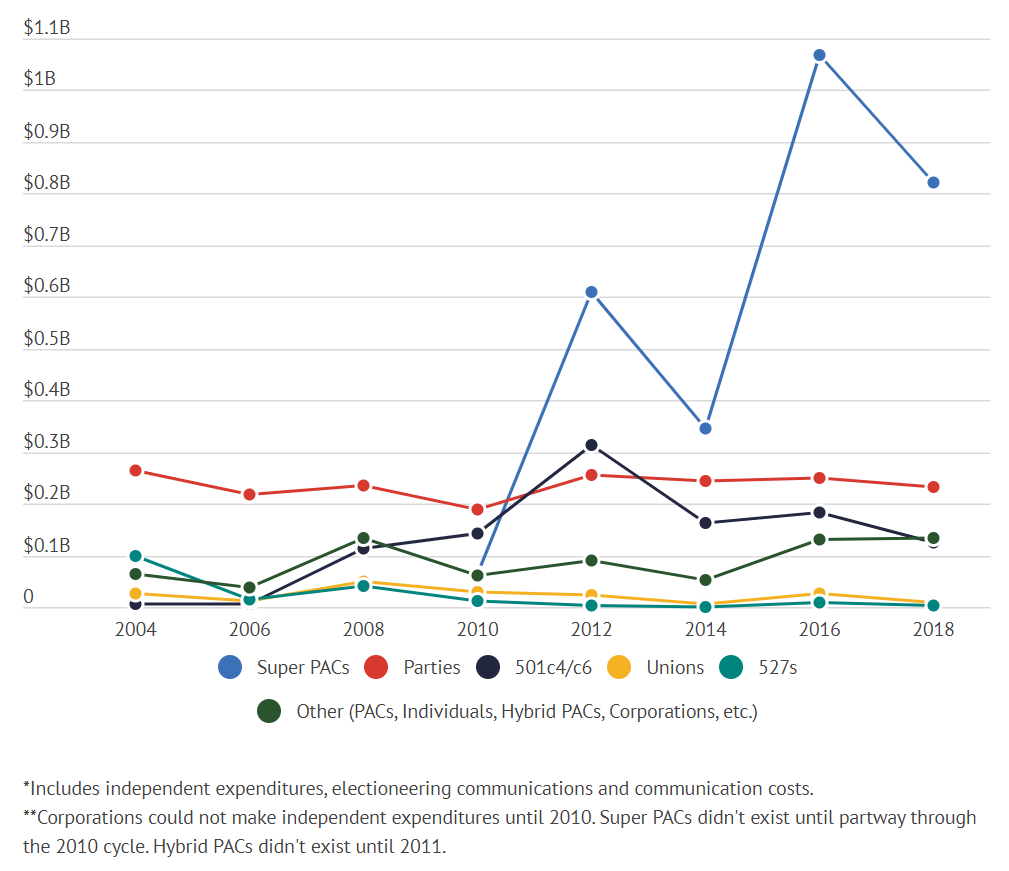
La explosión de gasto de los Super PACs seguida del fallo Citizens United v. FEC
El rol de la dark money (cont.)
- ¿Quiénes son algunos de los más importantes grupos de dark money?
- La Cámara de Comercio de EEUU; Crossroads GPS (Karl Rove); Americans for Prosperity (Koch Brothers)
- Un tema adicional es la influencia del dinero extranjero en las actividades de estos grupos –legalmente está prohibido donaciones de personas físicas y jurídicas extranjeras:
- La Cámara de Comercio de EEUU recibe dinero de membresía de empresas que representa –muchas incluso de propiedad extranjera
- La National Rifle Asociation, alineado con el partido republicano, recibe cuantiosas sumas de fabricantes extranjeros como SIG Sauer y Beretta
- El American Chemistry Council también tiene a muchas empresas extranjeras entre sus miembros
El lobbying como actividad
- El lobbying en EEUU está implicitamente (originalmente) aceptado a partir de la Primera Enmienda pero adoptó status legal en 1946 con la Federal Regulation of Lobbying Act que fue luego reemplazada por la Lobbying Disclosure Act de 1995
- La High Authority for Transparency in Public Life ha publicado un estudio para 41 países documentando las provisiones en relación a la actividad de lobbying
- Sólo 17 países tienen una ley nacional de lobby (regulación de intereses especiales)
- 22 países no tienen ley nacional de lobby
- El resto se rigen por leyes local o adhesión a leyes supranacionales
El lobbying como actividad (cont.)
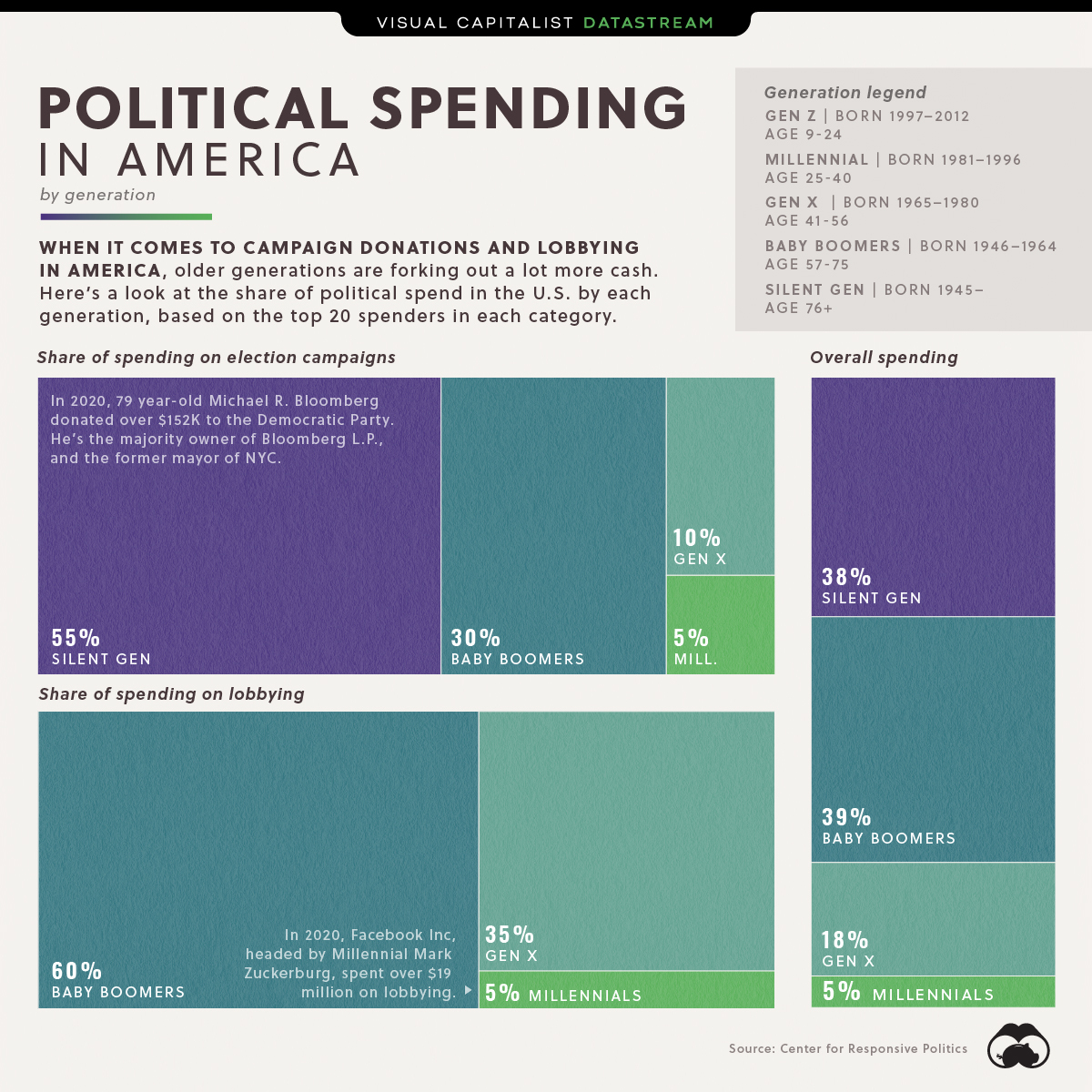
Composición del gastos en financiamiento de campañas y en lobbying por grupos etarios (generaciones)
Modelos básicos de competencia electoral con grupos de interés
Grupos de presión y poder político
- Ahora suponga que algunos grupos de individuos en la sociedad tienen capacidad de organizarse como grupos de presión (lobbies) y aportar contribuciones de campaña
- Todos los grupos tienen la misma densidad ideológica \(\phi{j}=\phi\) –el poder no proviene de su sensibilidad ideológica
- Variable \(O^{j}\) igual a 1 si grupo se organiza como lobby; 0 en caso contrario
- cada individuo de un lobby contribuye \(C^{j}_{P}\) recursos al candidato \(P\)
Grupos de presión y poder político (cont.)
- Cantidad total de fondos recibida por \(P\):
\[\begin{equation} C_{P}=\sum_{j=1}^{n} O^{j}\alpha^{j}C^{j}_{P} \end{equation}\]
- Suponemos que candidato recibe contribuciones luego de anunciar su plataforma de política pero antes que la preferencia general \(\delta\) sea conocida
Grupos de presión y poder político (cont.)
- Pero ahora \(\delta\) tiene dos componentes:
- \(\tilde{\delta}\) igual al modelo anterior
- componente \(h(C_{B}-C_{A})\) –introduce el hecho de que las contribuciones permiten mejorar popularidad general con un parametro de efectividad \(h\)
Grupos de presión y poder político (cont.)
- Entonces el nuevo votante pivotal (swing) de cada grupo será:
\[\begin{equation} \tilde{\sigma^{j}}=V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})-\tilde{\delta^{j}}+h(C_{B}-C_{A}) \end{equation}\]
- y encontramos que:
\[\begin{equation} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})=\frac{1}{2}+\psi \left[\sum_{j} \alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h(C_{A}-C_{B})\right] \end{equation}\]
Grupos de presión y poder político (cont.)
- Note la diferencia con modelos sin lobbies
- no sólo debemos encontrar comportamiento óptimo de los candidatos sino también el comportamiento óptimo de los diferentes lobbies
- En cierta forma los candidatos anticipan los incentivos de los lobbies para darles recursos y eso debería reflejarse en las propuestas de política
- Una funcion objetivo del lobbies puede ser maximizar utilidad esperada neta de contribuciones
Grupos de presión y poder político (cont.)
- Fn. objetivo de lobby \(j\) es:
\[\begin{equation} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})V^{j}(\mathbf{q_{A}})+(1-p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})V^{j}(\mathbf{q_{B}})-\frac{1}{2}\left((C^{j}_{B})^{2}+(C^{j}_{A})^{2}\right) \end{equation}\]
- cada grupo busca maximizar la utilidad que le genera cada candidato ponderando por la probabilidad de que cada candidato sea elegido neta de costos asociados a la contribucion
- ideología no juega; note que contribuciones ayudan a aumentar la probabilidad de ganar la eleccion
Grupos de presión y poder político (cont.)
- La CPO respecto a la contribución para \(A\)
\[\begin{equation} \frac{\partial{p_{A}}(\mathbf{q_{A}},\mathbf{q_{B}})}{\partial{C^{j}_{A}}}\left[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})\right]=C^{j}_{A} \end{equation}\]
- iguala el BMg de apoyar a \(A\) al CMg de proveer la contribución \(C^{j}_{A}\)
\[\begin{equation} C^{j}_{A}=\max \{0,h\psi\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]\} \end{equation}\]
Grupos de presión y poder político (cont.)
Problema de los candidatos. Candidatos consideran incentivos de lobbies al fijar plataforma dado que esta afecta cuantas contribuciones recien y a su vez esto incide sobre su probabilidad de ser elegidos. El problema es perfectamente simétrico y ambos candidatos convergen a la misma plataforma. Si no fuera así, un candidato puede atraer toda la contribución de algún lobby y el otro candidato movería su plataforma y así.
Grupos de presión y poder político (cont.)
- El candidato \(A\) elige la \(\mathbf{A}\) que maximiza:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h(\sum_{j}O^{j}\alpha^{j}C^{j}_{A}-\sum_{j}O^{j}\alpha^{j}C^{j}_{B})\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h\sum_{j}O^{j}\alpha^{j}(C^{j}_{A}-C^{j}_{B})\right] \end{align}\]
Grupos de presión y poder político (cont.)
- Sustituyendo las contribuciones óptimas de cada lobby:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h\sum_{j}O^{j}\alpha^{j}(h\psi\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})])\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h^{2}\psi\sum_{j}O^{j}\alpha^{j}(\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})])\right] \end{align}\]
Grupos de presión y poder político (cont.)
- Podemos tomar como dados todo lo que depende de \(\mathbf{q_{B}}\) y las constantes para maximizar:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=K+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})]+h^{2}\psi\sum_{j}O^{j}\alpha^{j}(\alpha^{j}[V^{j}(\mathbf{q_{A}})])\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=K+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})][1+h^{2}\psi O^{j}\alpha^{j}]\right] \end{align}\]
Grupos de presión y poder político (cont.)
La última ecuación muestra que el problema es equivalente a maximizar una función de bienestar social ponderada en donde la ponderación de cada grupo \(j\) viene dada por \(\alpha^{j}(1+h^{2}\psi O^{j}\alpha^{j})\). Si todos los grupos tienen igual tamaño y todos están organizados –\(\alpha^{j}=\alpha\) y \(O^{j}=1\), la solución coincide con el optimo utilitarista. De lo contrario, grupos más grandes recibirían mayor ponderación –i.e. costo marginal de contribuciones es creciente pero beneficio de contribuir es un bien público para todo el grupo. Grupos más grandes reducen tamaño promedio de contribución por miembro.
Grupos de presión y poder político (cont.)
- Candidatos tienden a dar más peso a: 1) grupos más grandes; 2) con mayor organización
- Si sólo los pobres se organizan, reciben mayor ponderación y “extraen” un mayor nivel de provisión de bien público –incluso mayor al óptimo (populismo no óptimo económicamente)
- Lo contrario si sólo los ricos se organizan
- ¿Qué grupos tendrán mayor probabilidad de organizarse? ¿Los pequeños? Posible menor problema de acción colectiva. ¿Los más grandes? ¿Los que más tienden a perder con una política pública? Beneficios concentrados, costos difusos.