Tópicos en Economía Política Moderna
Unidad 3. Competencia electoral. Modelos alternativos (cont)
If money go before, all ways do lie open.
[William Shakespeare, Ford, The Merry Wives of Windsor, Act 2 Scene 2 (1602)]
Financiamiento de campañas y lobbying
- Actividad pre-electoral y post-electoral
- Regulación versus desregulación
- ¿Comprando la política o comprando influencia?
Motivación
- ¿Cómo obtienen los grupos de interés especial su poder e influencia?
- ¿Qué determina el grado en que pueden afectar los resultados de las políticas?
- ¿Qué sucede cuando grupos con diferentes objetivos compiten por la influencia?
Según Grossman y Helpman (2001) un grupo de interés es cualquier grupo identificable de votantes con preferencias similares en un subconjunto de cuestiones políticas.
Financiamiento de campañas
Elecciones USA 2024. Estadísticas de financiación de campaña.
La Comisión Federal de Elecciones (FEC) es la agencia reguladora independiente encargada de administrar y hacer cumplir la ley federal de financiamiento de campañas. Dicha ley cubre tres temas amplios:
- Divulgación pública de los fondos recaudados y gastados para influir en las elecciones federales
- Restricciones a las contribuciones y gastos realizados para influir en las elecciones federales
- El financiamiento público de las campañas presidenciales
Financiamiento de campañas (cont.)
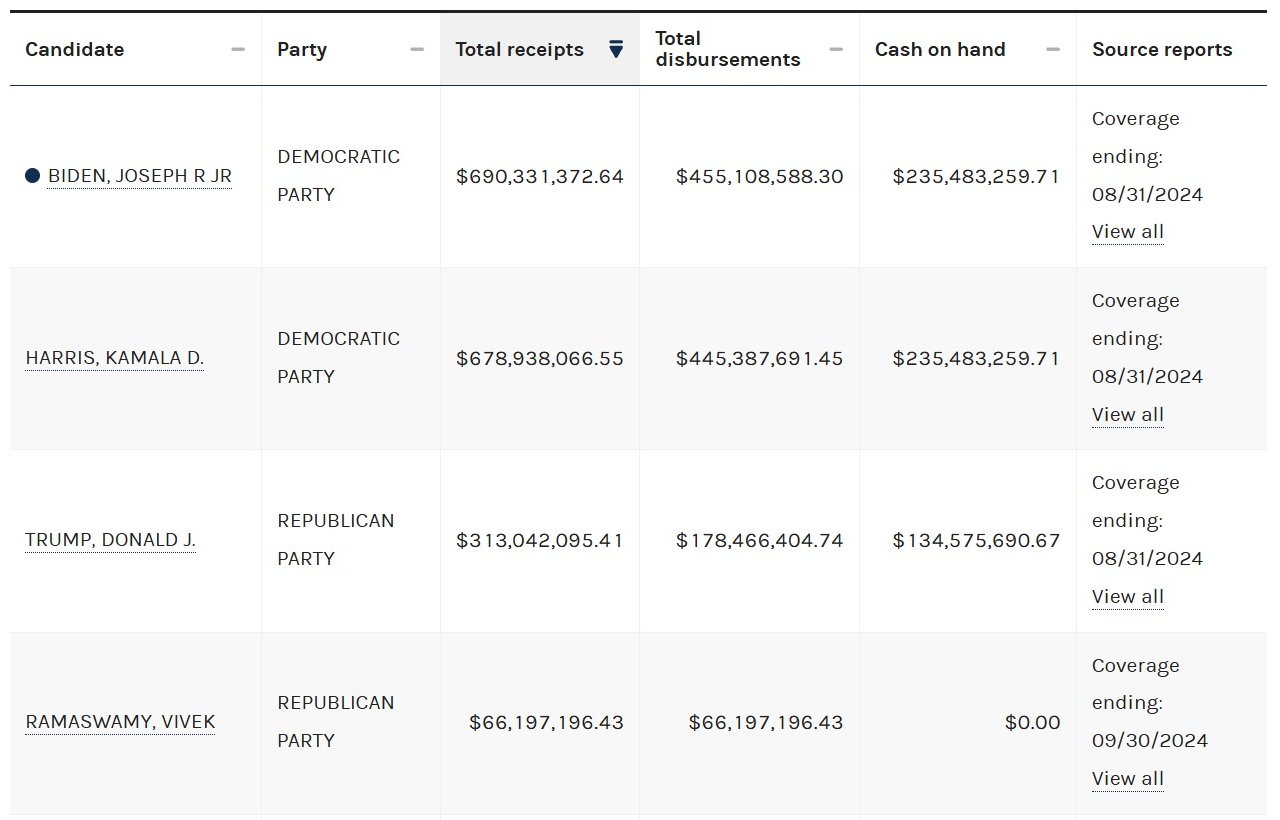
Financiamiento total de los candidatos
Financiamiento de campañas (cont.)
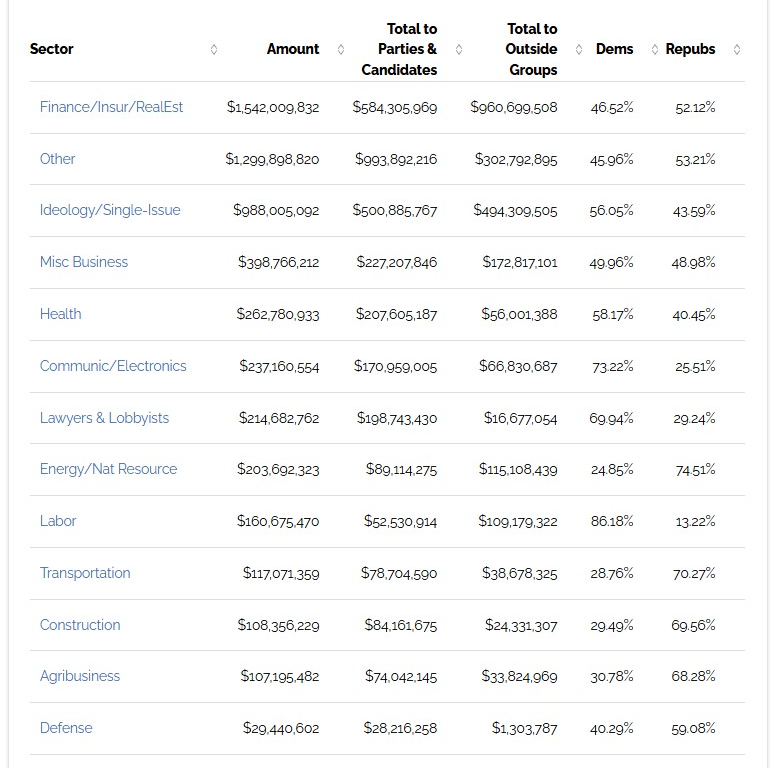
Grupos de interés. https://www.opensecrets.org/
Financiamiento de campañas (cont.)
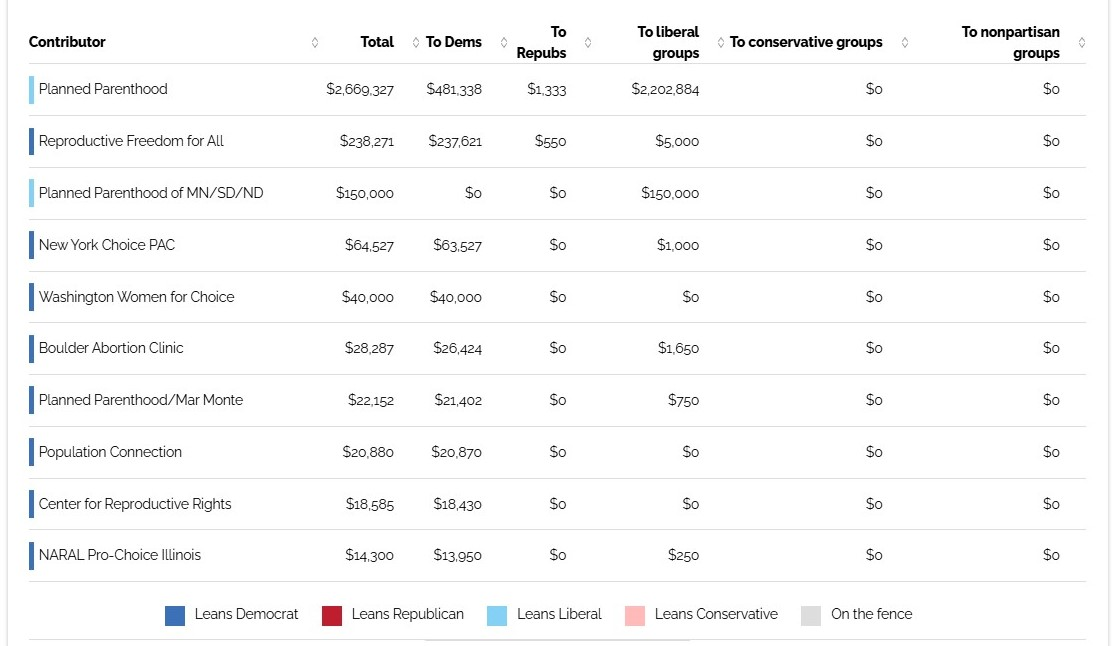
Pro-Abortion
Financiamiento de campañas (cont.)
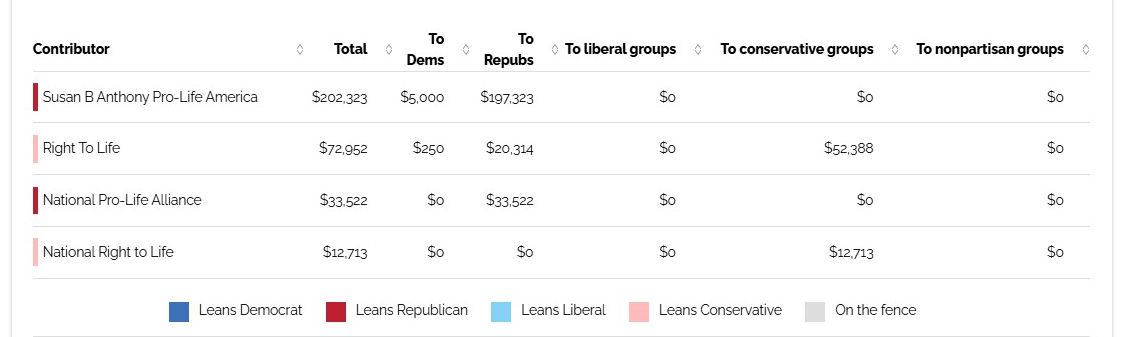
Anti-Abortion
Financiamiento de campañas (cont.)
- ¿Y por casa cómo andamos? En Argentina, las dos leyes más importantes que regulan la actividad electoral y el financiamiento de partidos politicos son la Ley 26571 (2009) –hito principal el establecimiento de las PASO- y la Ley 26215 (2007) y sus modificatorias
- ¿El lobbying está institucionalizado en Argentina? No!
- hay algunas iniciativas pero no hay una Ley Nacional
- Régimen de Acceso a la Información Pública (2003, luego Ley 27275 (2016))
Financiamiento de campañas (cont.)
- Importante notar la deficiencia en la sistematización, publicación y difusíon de estadísticas en relación a la actividad de financiamiento partidario
- Sin embargo, algunos avances en años recientes Link: Financiamiento de Campañas - Aportes privados
- En Argentina pueden aportar personas físicas y jurídicas –ambas con limitaciones. No pueden aportar personas físicas/jurídicas extranjeras y tampoco gobiernos y entidades públicas extranjeras
Financiamiento de campañas (cont.)
Contribuciones por sectores de actividad - Personas jurídicas
Gasto en publicidad
- El gasto en publicidad tradicional –principalmente radio y TV- puede consultarse en sitios que agregan y monitorean esta información: Gasto en publicidad tradicional
- Interesante mirar también la actividad de donación y contribuciones en forma de publicidad digital –gasto en publicidad digital tomando con fuente Google y Facebook
- Recurso útil: Gasto en publicidad digital
- Interesante correlacionar el gasto en publicidad digital con ultimo resultado electoral/encuestas de intención de voto
El rol de la dark money
- En lingo especialista, dark money refiere al gasto con intención de afectar los resultados políticos en el cual la fuente/origen de los fondos no es revelado
- En EEUU esto es posible por la existencia de ONGs políticamente activas (tipología 501(c)(4)) que no tienen obligacion de declarar sus donantes
- Esto “explotó” luego de 2010 de producido el fallo de la Corte “Citizens United v. FEC Supreme Court” – que basicamente permitió la existencia y proliferació de estas grupos políticamente activos
El rol de la dark money (cont.)
Citizens United v. FEC Supreme Court. En 2007, en FEC v. Wisconsing Right to Life la Corte Suprema falló que las organizaciones sin fines de lucro podía usar fondos para publicidad antes de las elecciones siempre y cuando estas publicidades no se expresaran explícitamente a favor (o en contra) de algún candidato. En el año 2010, la Corte Suprema falló que la prohibición que pesaba sobre contribuciones politicas independientes violaba el derecho a la libre expresión contenido en la Primera Enmienda. Este fallo permitió deliberadamente el uso de fondos para publicidad que se expresara explícitamente a favor (o en contra) de algún candidato. Desde este fallo, se produjo la década de mayor gasto en campañas en la historia de los EEUU.
El rol de la dark money (cont.)
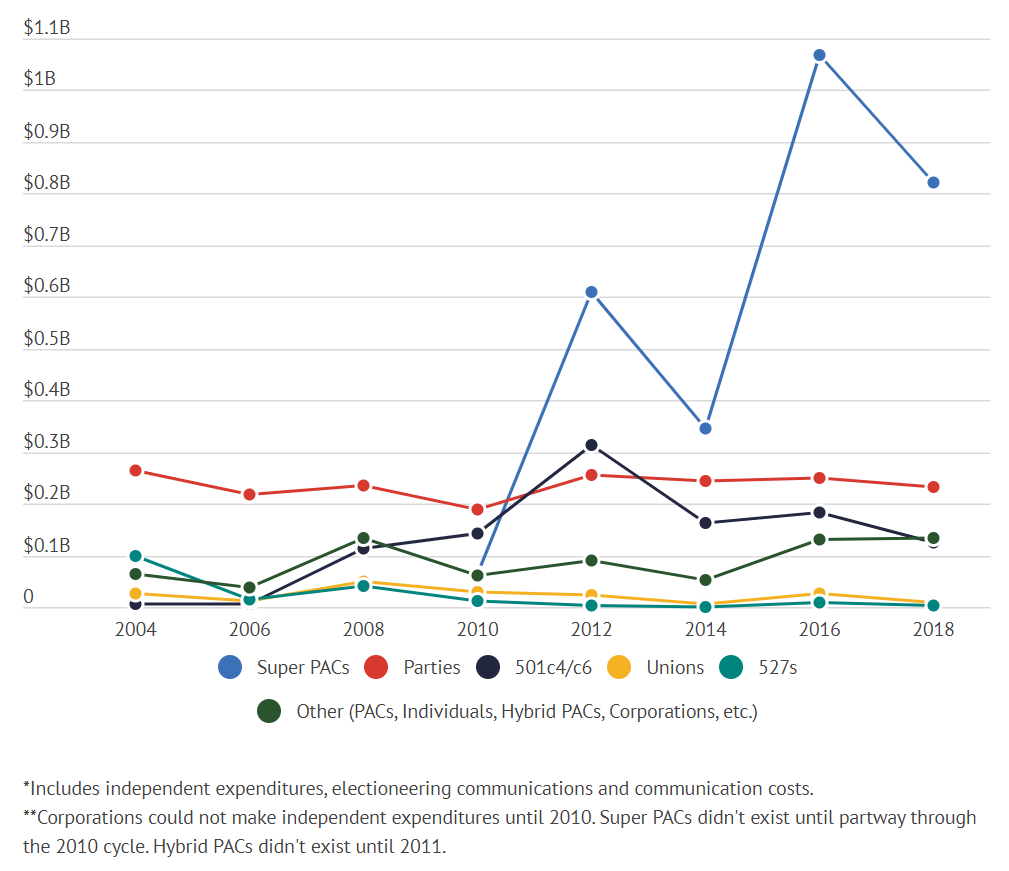
La explosión de gasto de los Super PACs seguida del fallo Citizens United v. FEC
El rol de la dark money (cont.)
- ¿Quiénes son algunos de los más importantes grupos de dark money?
- La Cámara de Comercio de EEUU; Crossroads GPS (Karl Rove); Americans for Prosperity (Koch Brothers)
- Un tema es la influencia del dinero extranjero en las actividades de estos grupos –legalmente está prohibido donaciones de personas extranjeras:
- La Cámara de Comercio de EEUU recibe dinero de membresía de empresas que representa –muchas incluso de propiedad extranjera
- La National Rifle Asociation, alineado con el partido republicano, recibe cuantiosas sumas de fabricantes extranjeros como SIG Sauer y Beretta
- El American Chemistry Council muchas empresas extranjeras entre miembros
El lobbying como actividad
- El lobbying en EEUU está implicitamente (originalmente) aceptado a partir de la Primera Enmienda pero adoptó status legal en 1946 con la Federal Regulation of Lobbying Act que fue luego reemplazada por la Lobbying Disclosure Act de 1995
- La High Authority for Transparency in Public Life ha publicado un estudio para 41 países documentando las provisiones en relación a la actividad de lobbying
- Sólo 17 países tienen una ley nacional de lobby (regulación de intereses especiales)
- 22 países no tienen ley nacional de lobby
- El resto se rigen por leyes local o adhesión a leyes supranacionales
El lobbying como actividad (cont.)
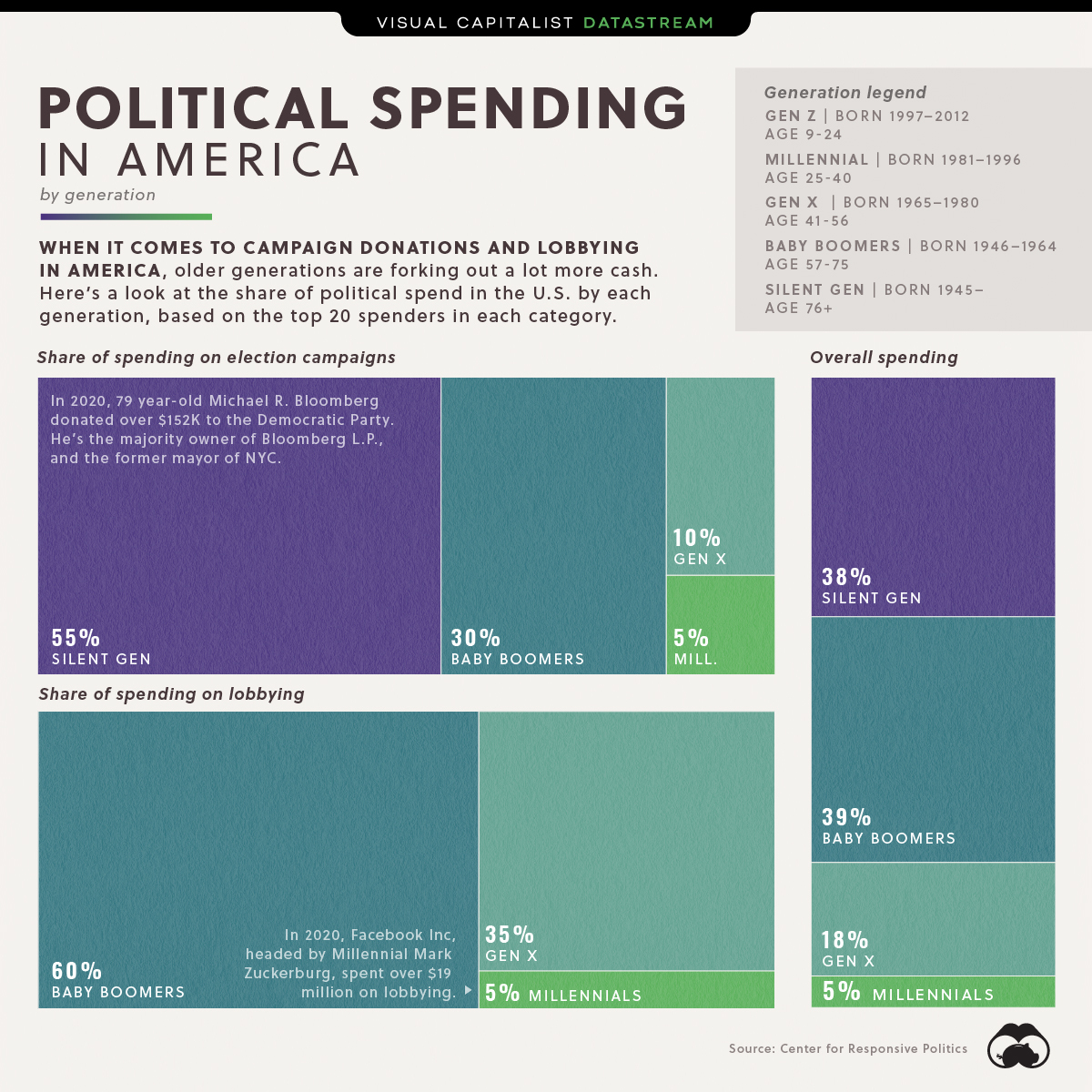
Composición del gastos en financiamiento de campañas y en lobbying por grupos etarios (generaciones)
Modelos básicos de competencia electoral con grupos de interés
Grupos de presión y poder político
- Ahora suponga que algunos grupos de individuos en la sociedad tienen capacidad de organizarse como grupos de presión (lobbies) y aportar contribuciones de campaña
- Todos los grupos tienen la misma densidad ideológica \(\phi{j}=\phi\) –el poder no proviene de su sensibilidad ideológica
- Variable \(O^{j}\) igual a 1 si grupo se organiza como lobby; 0 en caso contrario
- cada individuo de un lobby contribuye \(C^{j}_{P}\) recursos al candidato \(P\)
Grupos de presión y poder político (cont.)
- Cantidad total de fondos recibida por \(P\):
\[\begin{equation} C_{P}=\sum_{j=1}^{n} O^{j}\alpha^{j}C^{j}_{P} \end{equation}\]
- Suponemos que candidato recibe contribuciones luego de anunciar su plataforma de política pero antes que la preferencia general \(\delta\) sea conocida
Grupos de presión y poder político (cont.)
- Pero ahora \(\delta\) tiene dos componentes:
- \(\tilde{\delta}\) igual al modelo anterior
- componente \(h(C_{B}-C_{A})\) –introduce el hecho de que las contribuciones permiten mejorar popularidad general con un parametro de efectividad \(h\)
Grupos de presión y poder político (cont.)
- Entonces el nuevo votante pivotal (swing) de cada grupo será:
\[\begin{equation} \tilde{\sigma^{j}}=V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})-\tilde{\delta^{j}}+h(C_{B}-C_{A}) \end{equation}\]
- y encontramos que:
\[\begin{equation} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})=\frac{1}{2}+\psi \left[\sum_{j} \alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h(C_{A}-C_{B})\right] \end{equation}\]
Grupos de presión y poder político (cont.)
- Note la diferencia con modelos sin lobbies
- no sólo debemos encontrar comportamiento óptimo de los candidatos sino también el comportamiento óptimo de los diferentes lobbies
- En cierta forma los candidatos anticipan los incentivos de los lobbies para darles recursos y eso debería reflejarse en las propuestas de política
- Una funcion objetivo del lobbies puede ser maximizar utilidad esperada neta de contribuciones
Grupos de presión y poder político (cont.)
- Fn. objetivo de lobby \(j\) es:
\[\begin{equation} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})V^{j}(\mathbf{q_{A}})+(1-p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})V^{j}(\mathbf{q_{B}})-\frac{1}{2}\left((C^{j}_{B})^{2}+(C^{j}_{A})^{2}\right) \end{equation}\]
- cada grupo busca maximizar la utilidad que le genera cada candidato ponderando por la probabilidad de que cada candidato sea elegido neta de costos asociados a la contribucion
- ideología no juega; note que contribuciones ayudan a aumentar la probabilidad de ganar la eleccion
Grupos de presión y poder político (cont.)
- La CPO respecto a la contribución para \(A\)
\[\begin{equation} \frac{\partial{p_{A}}(\mathbf{q_{A}},\mathbf{q_{B}})}{\partial{C^{j}_{A}}}\left[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})\right]=C^{j}_{A} \end{equation}\]
- iguala el BMg de apoyar a \(A\) al CMg de proveer la contribución \(C^{j}_{A}\)
\[\begin{equation} C^{j}_{A}=\max \{0,h\psi\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]\} \end{equation}\]
Grupos de presión y poder político (cont.)
Problema de los candidatos. Candidatos consideran incentivos de lobbies al fijar plataforma dado que esta afecta cuantas contribuciones recien y a su vez esto incide sobre su probabilidad de ser elegidos. El problema es perfectamente simétrico y ambos candidatos convergen a la misma plataforma. Si no fuera así, un candidato puede atraer toda la contribución de algún lobby y el otro candidato movería su plataforma y así.
Grupos de presión y poder político (cont.)
- El candidato \(A\) elige la \(\mathbf{A}\) que maximiza:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h(\sum_{j}O^{j}\alpha^{j}C^{j}_{A}-\sum_{j}O^{j}\alpha^{j}C^{j}_{B})\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h\sum_{j}O^{j}\alpha^{j}(C^{j}_{A}-C^{j}_{B})\right] \end{align}\]
Grupos de presión y poder político (cont.)
- Sustituyendo las contribuciones óptimas de cada lobby:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h\sum_{j}O^{j}\alpha^{j}(h\psi\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})])\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=\frac{1}{2}+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})]+h^{2}\psi\sum_{j}O^{j}\alpha^{j}(\alpha^{j}[V^{j}(\mathbf{q_{A}})-V^{j}(\mathbf{q_{B}})])\right] \end{align}\]
Grupos de presión y poder político (cont.)
- Podemos tomar como dados todo lo que depende de \(\mathbf{q_{B}}\) y las constantes para maximizar:
\[\begin{align} p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=K+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})]+h^{2}\psi\sum_{j}O^{j}\alpha^{j}(\alpha^{j}[V^{j}(\mathbf{q_{A}})])\right] \\ p_{A}(\mathbf{q_{A}},\mathbf{q_{B}})&=K+\psi \left[\sum_{j}\alpha^{j}[V^{j}(\mathbf{q_{A}})][1+h^{2}\psi O^{j}\alpha^{j}]\right] \end{align}\]
Grupos de presión y poder político (cont.)
La última ecuación muestra que el problema es equivalente a maximizar una función de bienestar social ponderada en donde la ponderación de cada grupo \(j\) viene dada por \(\alpha^{j}(1+h^{2}\psi O^{j}\alpha^{j})\). Si todos los grupos tienen igual tamaño y todos están organizados –\(\alpha^{j}=\alpha\) y \(O^{j}=1\), la solución coincide con el optimo utilitarista. De lo contrario, grupos más grandes recibirían mayor ponderación –i.e. costo marginal de contribuciones es creciente pero beneficio de contribuir es un bien público para todo el grupo. Grupos más grandes reducen tamaño promedio de contribución por miembro.
Grupos de presión y poder político (cont.)
- Candidatos tienden a dar más peso a: 1) grupos más grandes; 2) con mayor organización
- Si sólo los pobres se organizan, reciben mayor ponderación y “extraen” un mayor nivel de provisión de bien público –incluso mayor al óptimo (populismo no óptimo económicamente)
- Lo contrario si sólo los ricos se organizan
- ¿Qué grupos tendrán mayor probabilidad de organizarse? ¿Los pequeños? Posible menor problema de acción colectiva. ¿Los más grandes? ¿Los que más tienden a perder con una política pública? Beneficios concentrados, costos difusos.
Un modelo de contribuciones de campaña y lobbying aplicado a datos de Argentina
El rompecabezas de Tullock: ¿por qué hay tan poco dinero en la política estadounidense?
En 1972, el gasto total de campaña en elecciones federales fue de aproximadamente $200 millones y el gasto total federal fue de $400 billones de dólares.
En 2000, el gasto total de campaña fue de $3 billones y el gasto total federal fue de $2 trillones de dólares.
El gobierno federal otorgó $134 billones en contratos de defensa en el 2000, mientras que las firmas contratistas de defensa e individuos asociados a éstas donaron solo alrededor de $13.2 millones.
En definitiva, el valor de las políticas aplicadas es mucho mayor a las contribuciones de campaña.
El rompecabezas de Tullock:
¿Qué pasa en Argentina?
En 2007, el gobierno nacional otorgó $886 millones en contratos públicos, mientras que el monto total de contribuciones de campaña de todas las empresas e individuos fue de $15 millones de pesos.
Los números para 2013 fueron de $1.62 billones y $17 millones de pesos, respectivamente
Motivación II - Conexiones informales
- ¿Cómo influencian los Grupos de Interés la política y las políticas en Argentina?
- Demoras en las Declaraciones Juradas Anticipadas de Importación (DJAI); el problema se solucionó en uno o dos días cuando el entonces jefe de gabinete tomó cartas en el asunto.
Motivación II - Conexiones informales
Canales de influencia
“En Argentina hay dos formas de ejercer influencia: una, más tradicional, a través de reuniones formales y líderes de opinión, y otra, relacionada directamente con las campañas políticas y la cantidad de contribuciones por debajo de la mesa a cambio de favores futuros”
Motivación III - Relevancia de las políticas
Cambios en el régimen de financiación de la política
Hubo tres reformas al régimen de financiación de la política en Argentina en los últimos 15 años:
- la primera estuvo para formalizar el sistema mixto de financiación de la política (2002);
- la segunda intentó incrementar la transparencia y accountability (2007);
- y la tercera prohibió contribuciones de empresas y otras personas jurídicas (2009).
Hay poco o nada de evidencia de cómo estos cambios impactaron en distintos resultados.
Motivación III - Relevancia de las políticas
Regulación de la actividad de lobby
En este momento hay un borrador de un proyecto de ley que regula la actividad de los grupos de interés. Se conoce públicamente como el proyecto “Ley de Lobby” aunque el proyecto oficial solamente extiende la práctica ya vigente de registrar audiencias de interés.
Literatura Relacionada
Literatura s/ contribuciones de campaña y roll-call voting [Green and Krasno (1988), Palda and Palda (1998), Ansolabehere et al (2003), Stratmann (2005)]
Competencia electoral con grupos especiales de interés (Special Interest Groups, SIG) Baron (1994), Grossman & Helpman (1992, 1996, 2001)
Más allá de financiamiento de campaña \(\longrightarrow\) conexiones políticas y la (i.e. puerta giratoria) [Vidal, Draca & Fons-Rosen (2012), Acemoglu et al (2016)]
Timing de las influencias políticas \(\longrightarrow\) You (2014): 50%del lobby en EEUU lleva la forma de lobby - i.e. después del voto en el Congreso.
Foco es en lobby sobre el PE, no el PL –evidencia de que las votaciones roll-call/nominales en Argentina son altamente partidistas [Jones (2001), Jones, Wang and Micozzi (2009)].
Lo que hacemos
- Creamos un modelo teórico donde los Grupos de Interés deciden una asignación óptima entre contribuciones ex-ante y ex-post con el objetivo de obtener la mayor cantidad de contratos públicos [listo]
- Testear (parcialmente) algunas de las implicancias teóricas con respecto al tamaño y la dirección de los efectos y las relaciones entre ambos canales de influencia [en proceso]
- Derivar implicancias de política contribuyendo al debate de las reformas institucionales [en proceso]
Intuición e implicancias
- Si Grupos de Interés tienen preferencias similares, las contribuciones ex-ante y ex-post son sustitutos perfectos.
- Mientras más alto sea el valor de los contratos públicos, más alto será el incentivo a involucrarse en lobby ex-post, que es costoso depende del valor de los contratos y del monto de contribuciones ex-ante
- Además, probablemente haya lugar para cooperación en vez de competencia entre Grupos de Interés (especialmente en las actividad de lobby ex-post) – i.e. evidencia de formación de Uniones Transitorias de Empresas (UTE) para licitaciones públicas.
- Si los Grupos de Interés tienen preferencias extremadamente opuestas, entonces no tienen incentivos a hacer lobby ex-post (costoso) si ya hicieron contribuciones ex-ante. Caso contrario, contribuyen un mínimo monto para lobby.
Modelo
- Juego de elección entre 2 candidatos, \(A\) y \(B\)
- \(A\) gana la elección con probabilidad \(P\); \(B\) con probabilidad \(1-P\).
- Gasto total en contratos públicos \(V^k>0\) para el candidato ganador \(k\), donde \(k=A,B\)
- Dos Grupos de Interés, \(i=1,2\). Pueden hacer:
- Contribuciones de campaña de la elección, \(C_i>0\)
- Contribuciones de lobby de la elección, \(L_i>0\)
- Los Grupos de Interés compiten ex-post para el mayor porcentaje, \(\alpha^k\), del gasto comprometido por el gobierno.
Timing
Resultado de la elección
- prob. de ganar la elección depende solamente del tamaño y dirección de las contribuciones de campaña ex-ante \(C_1\) y \(C_2\) \(\longrightarrow\) \(P(C_1,C_2)\) prob. que A gane la elección.
- Hay dos escenarios:
- “Preferencias alineadas” \(\longrightarrow\) ambos Grupos de Interés se alinean con el mismo candidato.
- “Preferencias opuestas” \(\longrightarrow\) los Grupos de Interés apoyan a candidatos diferentes. \[ U_i = P(C_i, C_j) \left(\alpha^A V^A - L^A_i \right) + \left(1 - P(C_i, C_j)\right) \left( \alpha^B V^B - L^B_i \right) - C_i \tag{1} \]
Resultado de la elección
donde la contribución total de campaña, \(C_i\) va al candidato que anuncia el mayor gasto en contratos públicos, \(V^k\).
La contribución propia de un Grupo de Interés es una externalidad positiva para él mismo en el periodo post-elección. Y ambas contribuciones (\(C_i\), \(L_i\)) son sustitutos intermporalmente.
Regla de asignación del gasto
Caso I: Preferencias Alineadas (AP)
- Si \(V^A>V^B\), las preferencias de ambos Grupos de Interés están alineadas. Cualquier contribución va al candidato A.
- Problema ex-post \(\longrightarrow\) ¿cuánto lobby ejercer después de la elección dado que un Grupo de Interés rival también hace lobby y dados \(C_i\) y \(C_j\)?
- Problema ex-ante \(\longrightarrow\) ¿cuántas contribuciones de campaña hacer dado el comportamiento óptimo de lobby ex-post?
Caso I: Preferencias Alineadas (cont.)
Proposición 1
Las contribuciones de lobby ex-post son crecientes en el nivel de gasto total \(V^k\), y si el candidato apoyado ex-ante:
gana la elección: las contribuciones ex-ante y ex-post son sustitutos perfectos: \(L^A_i + C^A_i = \frac{1}{4} V^A\), para: \(i=1,2\) y \(I=1\)
no gana la elección: \(L^B_i = \frac{1}{4} V^B\), para: \(i=1,2\) y \(I=0\).
En ambos casos, los porcentajes son \(\alpha^A= \alpha^B=\frac{1}{2}\)
Caso I: Preferencias Alineadas (cont.)
Proposición 2
Para A, existe un \(\check{V}^A < \hat{V}^A\) tal que las contribuciones ex-ante del Grupo de Interés exhiben una forma de U invertida con respecto al gasto de campaña de A, \(V^A\):
Caso I: Preferencias Alineadas (cont.)
Comportamiento Óptimo
Caso I: Preferencias Alineadas (cont.)
- Las contribuciones de campaña, \(C_i\) son un instrumento útil para sesgar la probabilidad de ganar de alguno de los candidatos; las contribuciones de lobby, \(L_i\) son (casi) un total derroche de recursos. –i.e \(\alpha^k\) no depende de éstas.
- Los Grupos de Interés pueden encontrar óptimo coordinar sus estrategias – especialmente, haciendo lobby. Pueden mejorar sus resultados al reducir sus contribuciones de lobby a un cierto mínimo.
Caso II: Preferencias Opuestas
- Contribuciones de campaña en direcciones opuestas\(\longrightarrow\) \(i\) dona a \(A\), \(j\) dona a \(B\).
- La única forma de incrementar la posibilidad de ganar para el candidato favorito de alguno de los Grupos de Interés es contribuir para él más que al otro.
- Asumimos que los Grupos de Interés obtienen utilidad sólo de que gane uno de los candidatos (preferencias opuestas extremas).
Proposición 3
En un juego con preferencias opuestas extremas, las contribuciones políticas se asignan a un único objetivo, sea la campaña o el lobby, de acuerdo con la siguiente regla:
Caso II: Preferencias Opuestas(Cont.)
Regla: Dado que el candidato favorito de \(i\) - el candidato \(A\) - ganó la elección:
- Si \(C_i>0\): no hay lobby ex-post y la utilidad del lobby ex-post está dada por \(\left( U^{EP}_i , U^{EP}_j \right)= \left( V^A , 0 \right)\)
- Si \(C_i=0\): el Grupo de Interés \(i\) es el único que hace lobby, particularmente \(L^A_i= \epsilon>0\), \(\epsilon \rightarrow 0\), y la utilidad del lobby ex-post está dada por \(\left( U^{EP}_i , U^{EP}_j \right)= \left( V^A-\epsilon , 0 \right)\).
Una regla análoga se verifica en el caso en que el candidato favorito de \(j\) (\(B\)) gana la elección, pero en ese caso \(j\) es el Grupo de Interés que alcanza un pago positivo.
Datos y metodología
- Datos compilados de distintas fuentes arriban a tres datasets principales, todos a un nivel de observación individual
- Datos de contribuciones de campaña \(\longrightarrow\) más de 46000 contribuciones individuales de campaña para elecciones nacionales desde 2003 a 2015 [Fuentes: Cámára Nacional Electoral]
- Datos de “audiencias de interés” \(\longrightarrow\) cerca de 70000 registros de audiencias entre miembros del Poder Ejecutivo, el gabinete, y directores e individuos representándose a sí mismos o a un grupo de interés organizado en el periodo 2003-2015. [Fuente: Registro Nacional de Audiencias de Interés]
- Datos de contratos públicos \(\longrightarrow\) incluye individuos y empresas participantes en contratos públicos de adquisición de bienes, servicios y obra pública. [Fuente: Boletin Oficial Nacional]
Datos: Dictionary databases
- Registros administrativos de AFIP (padrón de contribuyentes) \(\longrightarrow\) más de 4.6 millones de registros que contienen nombres e IDs (números de CUIT) para personas físicas y jurídicas. Códigos de actividad para 480000 entidades jurídicas.
- Personas jurídicas registradas y sus autoridades (Inspección General de Justicia) \(\longrightarrow\) más de 1.2 millones de registros que contienen números de CUIT y rol (socio, director, etc).
- Sistema Integrado Previsional Argentino (SIPA) \(\longrightarrow\) registros administrativos sobre el tamaño y el tipo de empresas.
Uniendo los IDs
- Identificador único común en todas las bases de datos \(\longrightarrow\) número de CUIT.
- Muchos datos faltantes de CUIT – es un problema fundamentalmente de las bases de datos de contrataciones públicas y audiencias de interés.
- Los datos crudos de contratos públicos tomados del Boletín Oficial contenían solamente el 15% de los datos de CUIT. Dado que los contratos públicos pueden otorgarse tanto a personas físicas como jurídicas, no es posible conocer con exactitud a quién se le otorgó el contrato.
- Cuando el CUIT está disponible, unir los datos es sencillo – exacto.
- Cuando el CUIT está faltante, seguimos dos procedimientos:
- Recupero manual de datos de CUIT \(\longrightarrow\) String-matching (matching basado en un “nombre”) contra una base de datos “diccionario” (dictionary database).
Algunos datos descriptivos
Algunos datos descriptivos (cont.)
Algunos datos descriptivos (cont.)
Algunos datos descriptivos (cont.)
Algunos datos descriptivos (cont.)
Algunos datos descriptivos (cont.)

Algunos datos descriptivos (cont.)

Algunos datos descriptivos (cont.)
Estrategia empírica
- Dos tipos de analisis: \[ Y_{i}=\sum_{h=0}^{H}y_{i,t+h}=\alpha+\beta C_{i,E}+\gamma \sum_{h=0}^{H} \omega_{t+h}L_{i,t+h}+\epsilon_{i} \tag{2} \]
- solamente usamos información de los actores que obtuvieron un número positivo de contratos públicos, tal que \(\beta\) y \(\gamma\) reflejan la existencia de correlación con la variable dependiente; esperamos que ambos coeficientes sean positivos.
Estrategia empírica (cont.)
- Para la submuestra en la cual tenemos tanto ganadores como perdedores de un contrato público dado, la especificación (1) puede ser estimada con la variable Y definida tal que tome dos valores posibles, 1 cuando un actor de interés obtuvo al menos un contrato público, y 0 en caso contrario.
\[ P_{i,j}=\alpha+\beta f(C_{i \in j,E})+\gamma h(L_{i \in j,t+h})+\epsilon_{i} \tag{3} \]
- donde \(j\) identifica un proceso de subasta específico; \(f(.)\) y \(h(.)\) son funciones que modelan las relaciones entre las contribuciones de campaña y los esfuerzos de lobby entre todos los actores de interés que participaron en los procesos de subasta, \(j (i \in j)\). La variable \(P_{i,j}\) toma el valor de 1 si el actor de interés \(i\) ganó el proceso de subasta, y 0 en caso contrario
Resultados
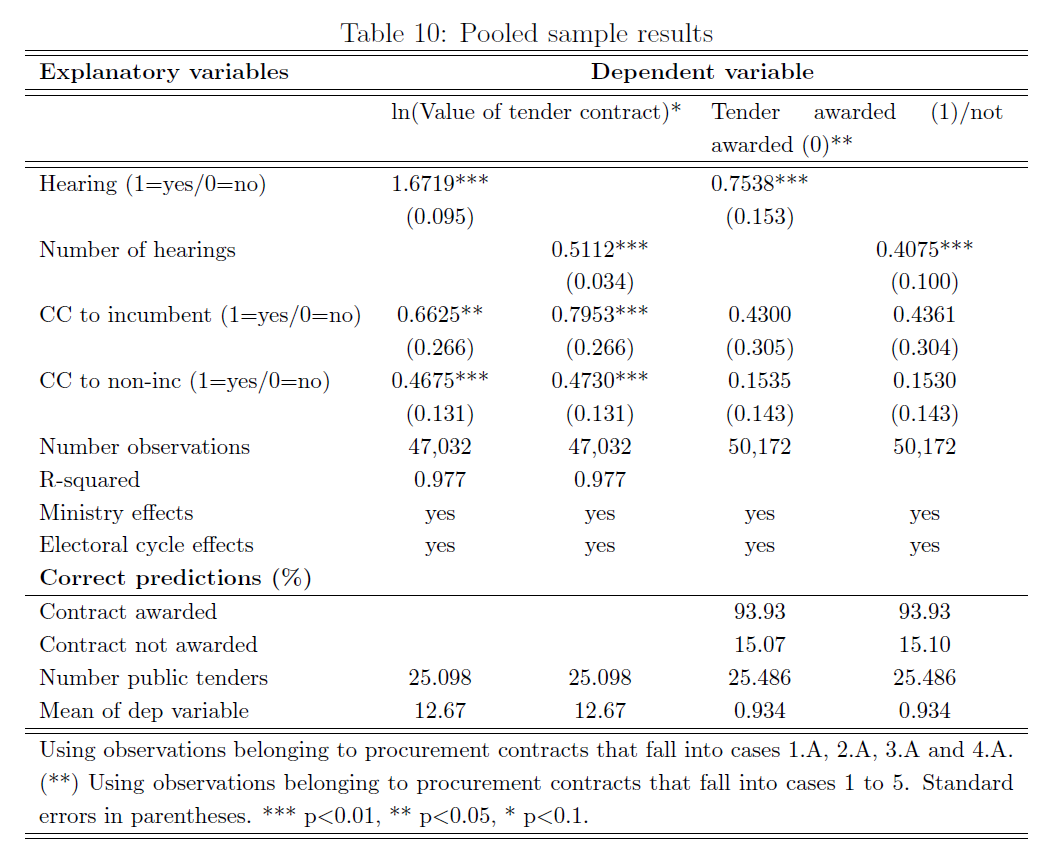
Resultados (cont.)
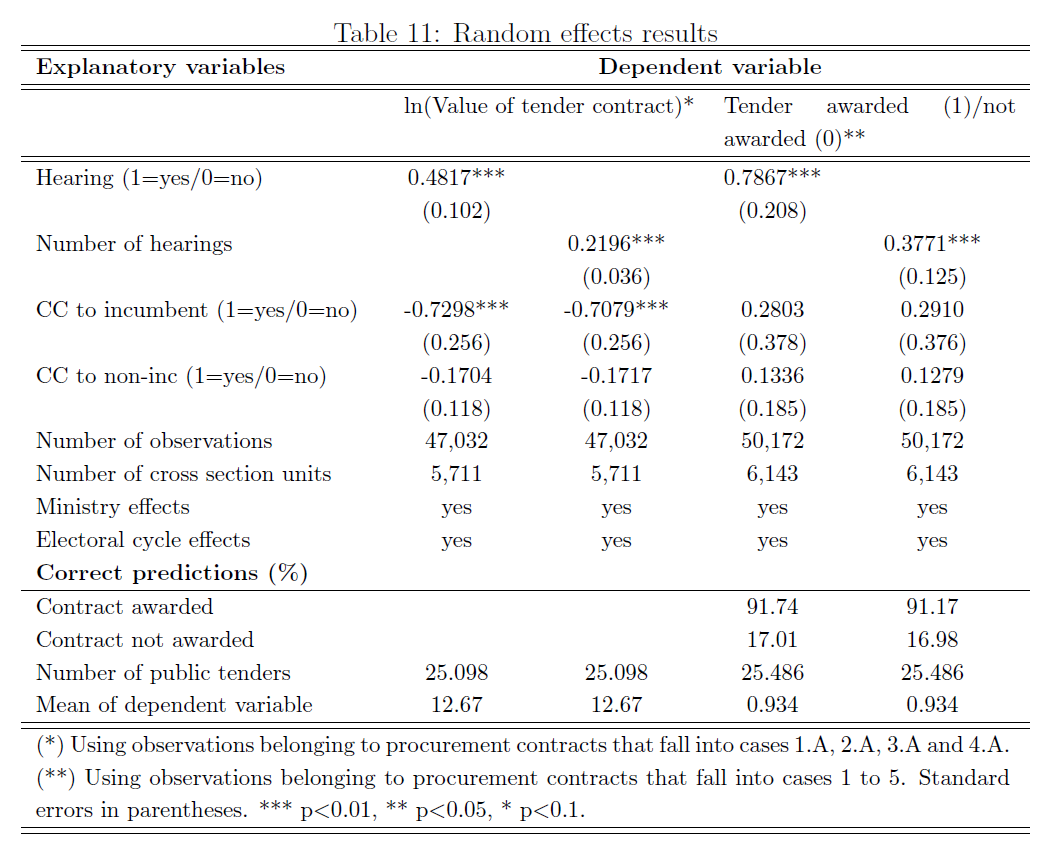
Resultados (cont.)
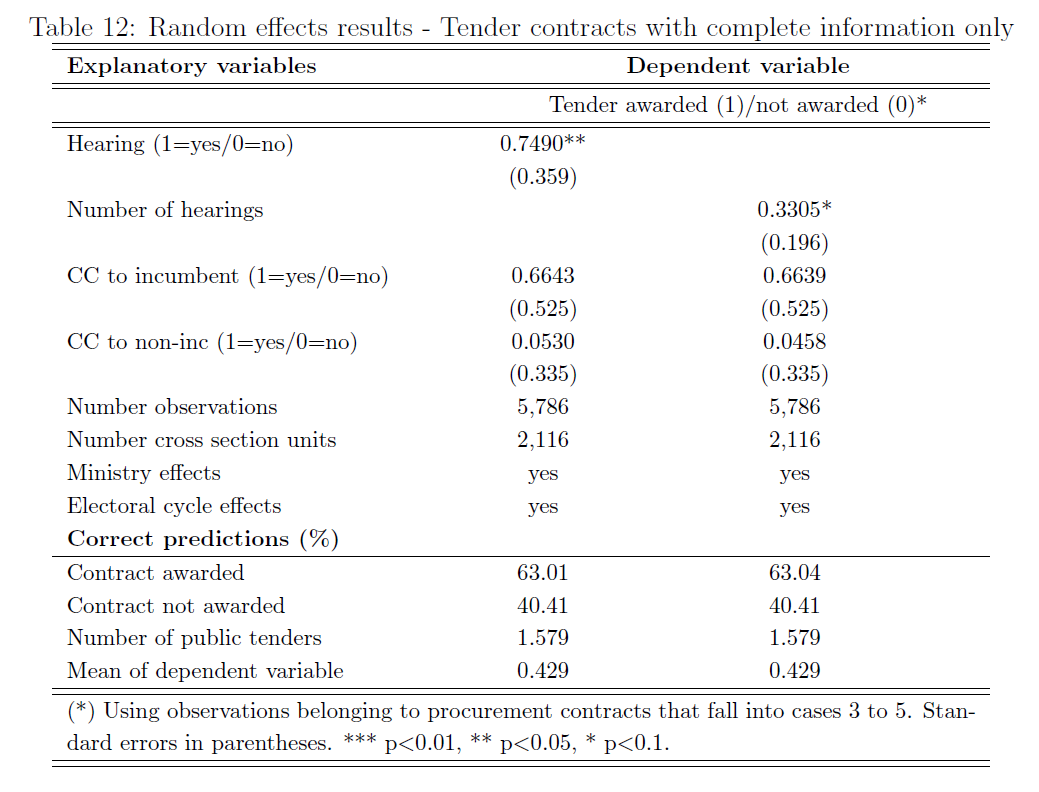
Resultados (cont.)
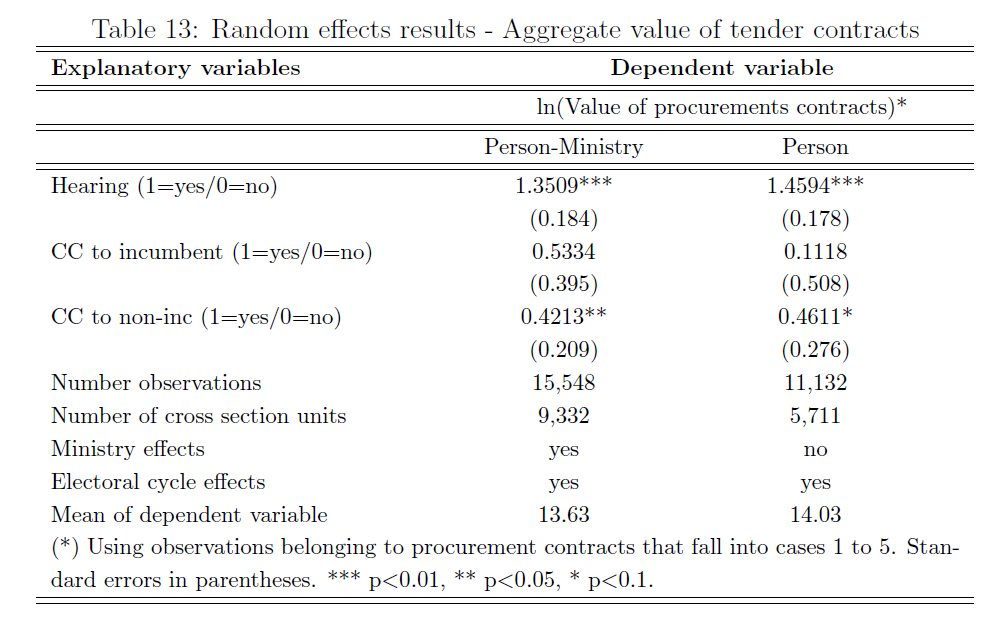
Resultados
- Tanto las contribuciones de campaña como las audiencias de lobby están positivamente asociados con licitaciones de mayores montos
- Asimismo, las audiencias de lobby están positivamente correlacionadas con la probabilidad de obtener un contrato (licitación)
- Evidencia sugerente de que el lobby sobre el PE en Argentina es importante y toma más la forma de audiencias de lobby que de contribuciones de campaña –OJO! puede haber tema de missing data!
Conexiones políticas y personales. Endorsements
Endorsement
- La bibliografía existente sobre los efectos del endorsement es ante todo teórica y enfocada en grupos de interés.
- Los modelos plantean que los individuos desinformados eligen a quién votar según señales que envían los grupos de interés.
- Según Grossman y Helpman (1999):
Endorsements are a simple language for communication between interest-group leaders and group members. The members, who share policy concerns, may not perfectly understand where their interests lie on certain issues. If their leaders cannot fully explain the issues, they can convey some information by endorsing a candidate or party
Endorsement y celebridades
- Estimar empíricamente el endorsement es difícil.
- Craig Garthwaite y Timothy J. Moore (2012) presentaron un trabajo novedoso preguntándose si el apoyo de celebridades a candidatos políticos puede tener efectos en el resultado de una elección.
- Los autores parten de un hecho concreto: el apoyo que le brindó Oprah Winfrey a Barack Obama en las elecciones primarias del partido demócrata en 2008.
Endorsement y celebridades: Caso Oprah-Obama
- Obama fue apoyado por Oprah tres meses después que anunciará su candidatura.
- Los autores observaron que este caso presentaba una oportunidad única porque existen indicadores para medir la popularidad e influciencia de la presentadora de televsión.
- Para poder llevar a cabo el experimiento, utilizan como indicadores: las suscripciones a la revista de Oprah y la venta de libros que ella recomienda.
- Las conclusiones a las que llegan son:
- El apoyo aumentó la participación electoral y las contribuciones de campaña de Obama.
- Oprah fue responsable de aproximadamente un millón de votos adicionales para Obama.
Endorsement y celebridades: Caso Taylor Swift
- El pasado 11 de septiembre, Taylor Swift publicó un post en instagram dando su apoyo a Kamala Harris (candidata a presidente en Estados Unidos).
- Según el portal de noticias CBS News, 405,999 usuarios visitaron la página vote.org a través del enlace que publicó Taylor.
- Los candidatos demócratas aprovecharon el apoyo de la cantante y comenzaron a vender friendship bracelets.